This post is the continuation of the Previous Post (Graphical Representation of Data Part 1).
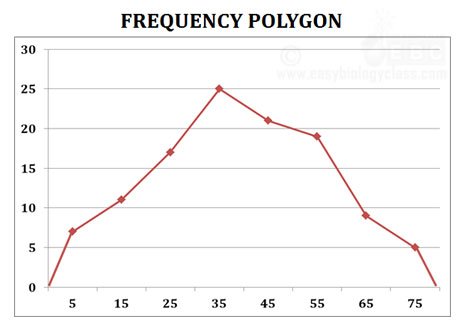
(3). Frequency Polygon
Ø The Frequency Polygon is a curve representing a frequency distribution.
Ø In frequency polygon, the mid values of each class are first obtained.
Ø In a graph paper, the frequency of each class is plotted against the mid-value of class (on the X axis).
Ø Then these points are then joined by a straight line.
Ø This straight line is extended in both directions to meet on the X axis.
Ø The first point is joined to the lower limit of the first class and the last point is joined to the upper limit of last class. Thus, the frequency polygon is a closed graph.
Ø The graph now obtained is called Frequency polygon.
Example: Construct a Frequency Polygon using the following data

Solution: Find the mid-value of each class
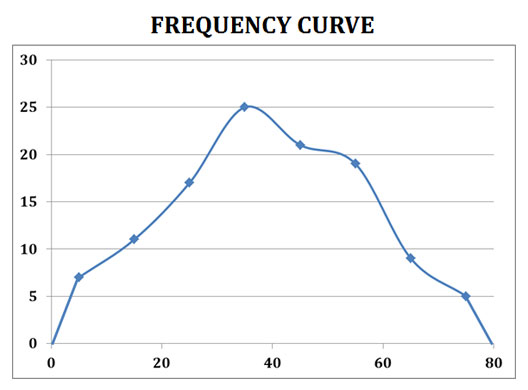
(4). Frequency curve
Ø The construction of a frequency curve is similar to that of a frequency polygon.
Ø Here the points of frequencies in the graph are connected by a free-hand smooth curve.
Ø Thus frequency curve is also called as ‘smoothed frequency curve’.
Ø The frequency curve also begins and ends in base line (X axis).
Ø Advantage: More smooth appearance of data than frequency polygon.
Example: Construct a Frequency Polygon using the following data

Solution: Find the mid-value of each class and plot against frequency.
(5). Ogive
Ø The ogive is a cumulative frequency curve.
Ø It is a free-hand graph showing the curve of a cumulative frequency.
Ø The ogive is constructed by plotting the upper class limit on the X axis and the corresponding cumulative frequency on the Y axis.
Ø Ogive is best used when the total frequency at any given time is to be displayed.
Ø There are TWO types of ogives:
(1). Less than ogive
(2). Greater than ogive (more than ogive)
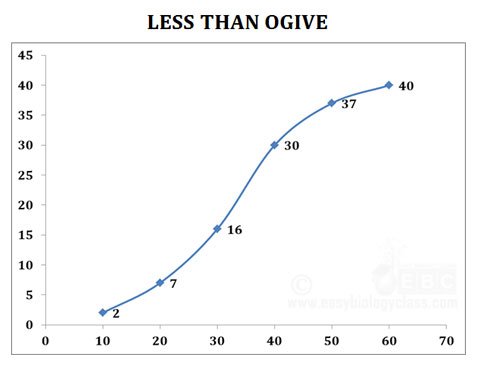
(1). Less than Ogive
Ø Less than ogive is the graph of the less than cumulative frequency distribution which shows the number of observations LESS THAN the upper class limit.
Ø First we calculate the cumulative frequency from the above (as usual).
Ø Then plot the upper class limit of class interval against the value of corresponding cumulative frequency.
Ø The points are joined by a free-hand smooth curve.
Ø The lower point of the curve is joined to the X-axis at the lower limit of the first class interval.
Example: Construct a less than ogive using the following data

Solution: Find the lower class limit and cumulative frequency. Then plot the lower class limit against the cumulative frequency.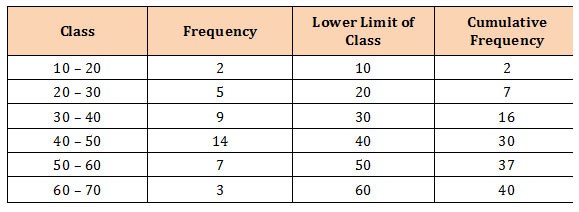
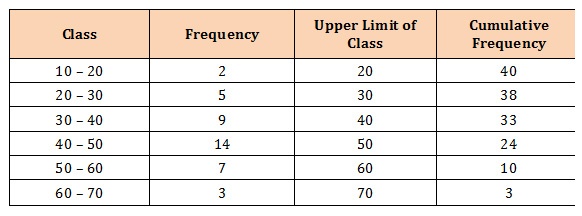
(2). Greater than ogive
Ø Greater than ogive is the graph of the greater than cumulative frequency distribution which shows the number of observations GREATER THAN the lower class limit.
Ø First, the frequencies are cumulated from below
Ø Then the cumulated frequency is plotted against the lower limit of the corresponding class interval.
Ø The uppermost point is joined with the Y-axis at the upper limit of the last class.
Example: Construct a greater than ogive using the following data

Solution: Find the upper class limit and cumulative frequency from below. Then plot the upper class limit against the cumulative frequency.
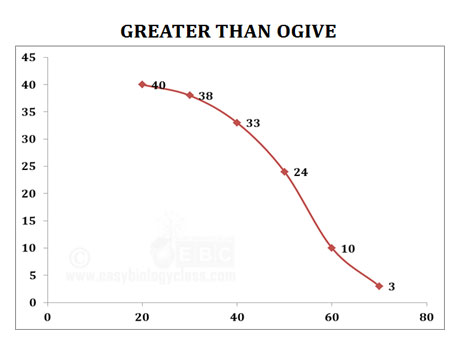
Calculating Median from Ogive
Ø Median of the frequency distribution can be calculated from the ogive with a quick method.
Ø First, draw a less than ogive and then draw a greater than ogive of the same data on same graph paper.
Ø The two curves will intercept at some point.
Ø A perpendicular line is drawn from the point of interception to the X-axis.
Ø This value on the X axis will be the median of the frequency distribution.
(6). Pie Chart
Ø The pie chart is also called as the circle graph or area diagram
Ø The pie chart makes the use of sectors in a circle to represent different categories of data.
Ø The circle has a total area of 360o which can be divided into component sectors based on the given data.
Ø The arc length of each sector is proportional to the frequency of the data.
Ø Arc length is proportional to central angle and the area of sector.
How to construct a Pie chart
Ø Calculate the angle of each sector (class) corresponding the frequency using the formula
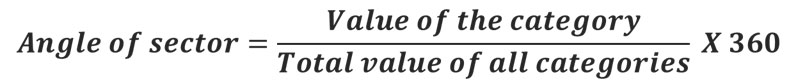
Ø Draw a circle of any radius and mark the centre.
Ø Mark the angles of each sector accurately
Ø Sectors can be then labeled or shaded to denote different classes.
Example: Construct a pie diagram using the following data
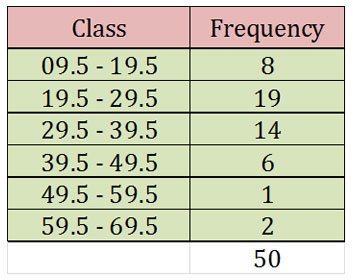
Solution: First calculate the angle of each sector using the above equation.
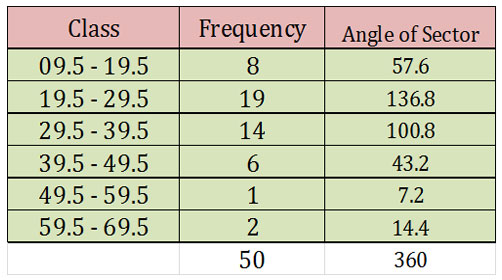
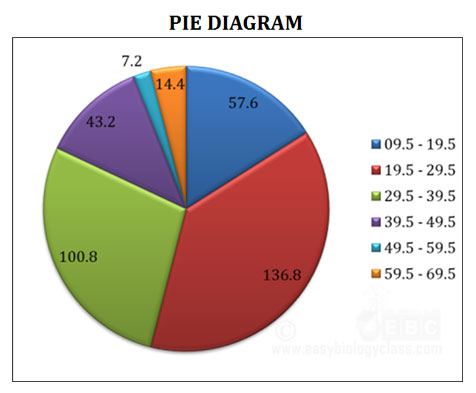
Ø The pie diagram can also be drawn using relative frequency using the formula
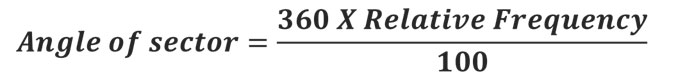
Ø Relative frequency: The frequency expressed as a fraction of the total frequency and the fraction of the obtained frequency.
Ø The relative frequency is expressed as the percentage.
<< Back to BIOSTATISTICS Notes

